Login
首页 全部课程 资源下载 系统课 图书馆 精选好文 聚客社区 关于我们
首页 > 精选好文 > AI大模型

神经网络基础深度解析：从感知机到反向传播

聚客AI 2025-06-06 12:59:57 人看过

本文系统讲解神经网络核心原理，涵盖感知机模型、激活函数、损失函数和反向传播算法，结合数学推导、可视化图解和代码实现，帮你彻底掌握神经网络工作机制。


一、感知机：神经网络的基石

1.1 感知机模型原理

import numpy as np
import matplotlib.pyplot as plt
class Perceptron:
    def __init__(self, input_size, lr=0.01):
        self.weights = np.random.randn(input_size)
        self.bias = np.random.randn()
        self.lr = lr
    
    def activate(self, x):
        # 阶跃函数
        return 1 if x >= 0 else 0
    
    def forward(self, inputs):
        summation = np.dot(inputs, self.weights) + self.bias
        return self.activate(summation)
    
    def train(self, inputs, target):
        prediction = self.forward(inputs)
        error = target - prediction
        
        # 权重更新
        self.weights += self.lr * error * inputs
        self.bias += self.lr * error
        
        return error
# 创建AND逻辑数据集
X = np.array([[0,0], [0,1], [1,0], [1,1]])
y = np.array([0, 0, 0, 1])
# 训练感知机
perceptron = Perceptron(input_size=2, lr=0.1)
epochs = 10
for epoch in range(epochs):
    errors = 0
    for i in range(len(X)):
        error = perceptron.train(X[i], y[i])
        errors += abs(error)
    
    print(f"Epoch {epoch+1}, Total Error: {errors}")
    if errors == 0:
        break
# 测试感知机
print("\n测试结果:")
for i in range(len(X)):
    pred = perceptron.forward(X[i])
    print(f"输入: {X[i]}, 预测: {pred}, 期望: {y[i]}")

1.2 感知机决策边界可视化

# 可视化决策边界
x_min, x_max = -0.5, 1.5
y_min, y_max = -0.5, 1.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
                     np.arange(y_min, y_max, 0.01))
Z = np.array([perceptron.forward(np.array([x, y])) 
              for x, y in zip(xx.ravel(), yy.ravel())])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(8,6))
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:,0], X[:,1], c=y, s=100, edgecolors='k')
plt.title("感知机决策边界")
plt.xlabel("输入1")
plt.ylabel("输入2")
plt.grid(True)
plt.show()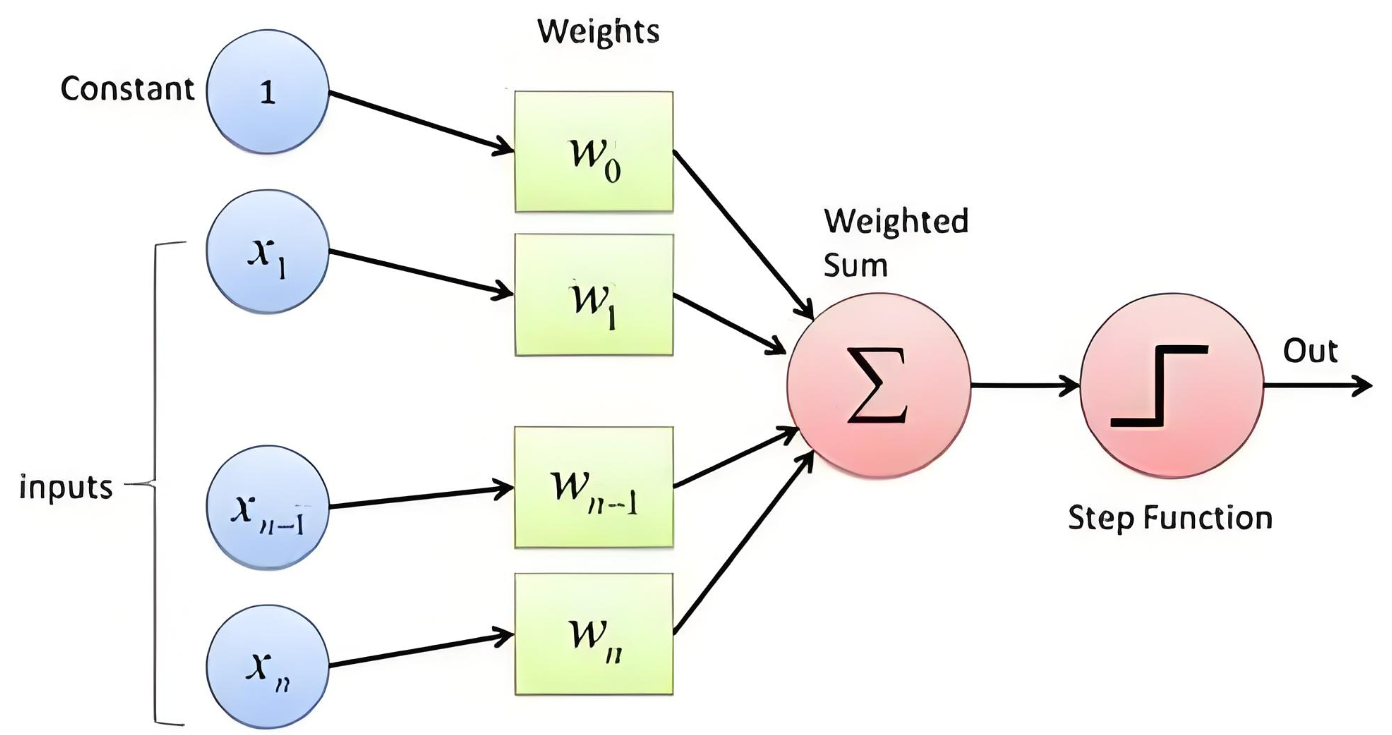

image.png

数学原理：

输出 = f(w·x + b)
其中：
w = 权重向量
x = 输入向量
b = 偏置项
f = 激活函数（阶跃函数）


二、激活函数：引入非线性能力

2.1 常用激活函数对比

import torch
import torch.nn.functional as F
# 定义常用激活函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
def relu(x):
    return np.maximum(0, x)
def tanh(x):
    return np.tanh(x)
def softmax(x):
    exp_x = np.exp(x - np.max(x))
    return exp_x / exp_x.sum(axis=0)
# 可视化
x = np.linspace(-5, 5, 100)
plt.figure(figsize=(12, 8))
plt.subplot(2, 2, 1)
plt.plot(x, sigmoid(x))
plt.title("Sigmoid"), plt.grid(True)
plt.subplot(2, 2, 2)
plt.plot(x, relu(x))
plt.title("ReLU"), plt.grid(True)
plt.subplot(2, 2, 3)
plt.plot(x, tanh(x))
plt.title("Tanh"), plt.grid(True)
plt.subplot(2, 2, 4)
plt.plot(x, softmax(x))
plt.title("Softmax"), plt.grid(True)
plt.tight_layout()
plt.show()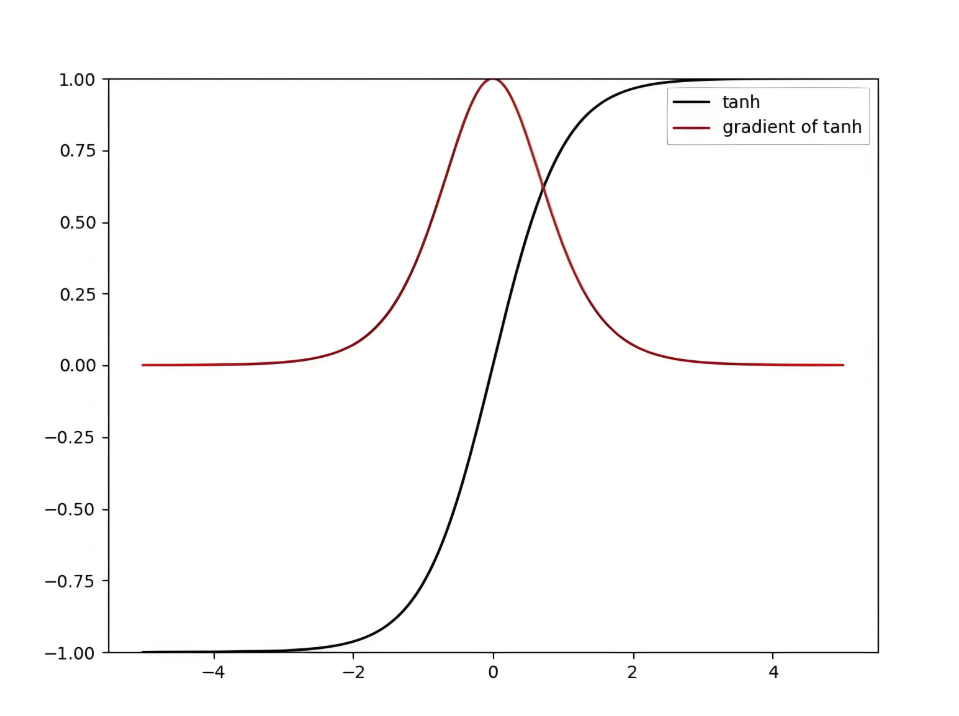

image.png

2.2 激活函数特性对比

image.png

2.3 激活函数导数实现

# 激活函数导数
def sigmoid_derivative(x):
    s = sigmoid(x)
    return s * (1 - s)
def relu_derivative(x):
    return np.where(x > 0, 1, 0)
def tanh_derivative(x):
    return 1 - np.tanh(x)**2
# 可视化导数
x = np.linspace(-3, 3, 100)
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.plot(x, sigmoid_derivative(x))
plt.title("Sigmoid导数")
plt.subplot(1, 3, 2)
plt.plot(x, relu_derivative(x))
plt.title("ReLU导数")
plt.subplot(1, 3, 3)
plt.plot(x, tanh_derivative(x))
plt.title("Tanh导数")
plt.tight_layout()
plt.show()


三、损失函数：衡量模型预测误差

3.1 常用损失函数实现

# 均方误差 (MSE)
def mse_loss(y_true, y_pred):
    return np.mean((y_true - y_pred)**2)
# 交叉熵损失
def cross_entropy_loss(y_true, y_pred, epsilon=1e-12):
    y_pred = np.clip(y_pred, epsilon, 1. - epsilon)
    return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
# 分类交叉熵
def categorical_crossentropy(y_true, y_pred, epsilon=1e-12):
    y_pred = np.clip(y_pred, epsilon, 1. - epsilon)
    return -np.sum(y_true * np.log(y_pred)) / y_true.shape[0]
# 可视化损失函数
y_true = np.array([1, 0, 1])
y_pred = np.linspace(0, 1, 100)
# MSE可视化
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.plot(y_pred, mse_loss(np.array([1]*100), y_pred))
plt.title("MSE (y_true=1)")
plt.xlabel("预测值"), plt.ylabel("损失")
# 二分类交叉熵
plt.subplot(1, 3, 2)
plt.plot(y_pred, cross_entropy_loss(np.array([1]*100), y_pred))
plt.title("二分类交叉熵 (y_true=1)")
# 多分类交叉熵
plt.subplot(1, 3, 3)
y_true_multi = np.eye(3)  # 3个类别的one-hot编码
y_pred_multi = np.array([np.linspace(0.01, 0.99, 100)]*3).T
losses = [categorical_crossentropy(y_true_multi, np.array([p, (1-p)/2, (1-p)/2])) for p in y_pred]
plt.plot(y_pred, losses)
plt.title("多分类交叉熵 (真实类别0)")
plt.tight_layout()
plt.show()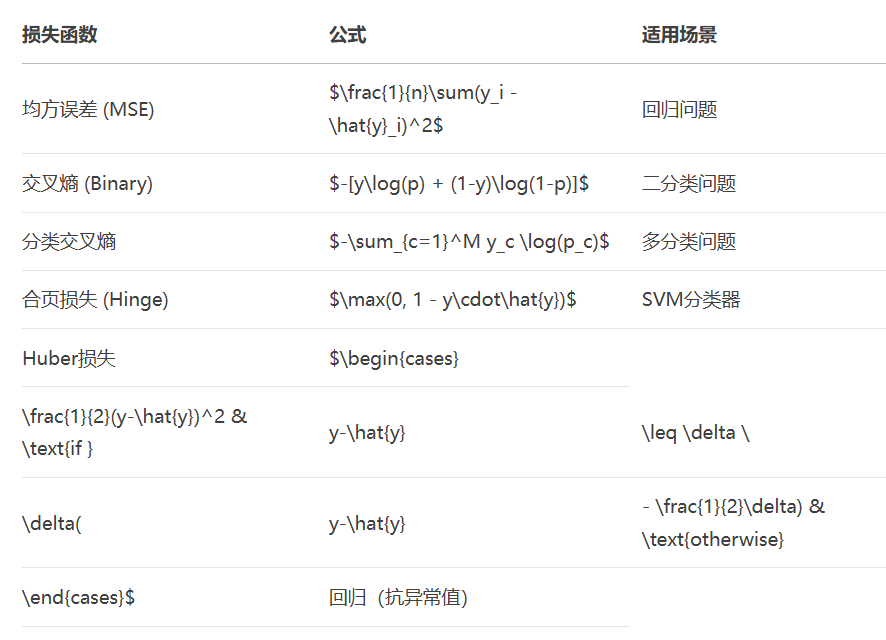

3.2 损失函数特性对比

image.png


四、反向传播：神经网络优化核心

4.1 反向传播数学原理

考虑一个简单网络：

输入层 (x) → 隐藏层 (h = σ(W1·x + b1)) → 输出层 (y = W2·h + b2)
损失函数 L = 1/2(y - t)^2

反向传播公式推导：

输出层梯度：

$\frac{\partial L}{\partial y} = y - t$
$\frac{\partial L}{\partial W2} = \frac{\partial L}{\partial y} \cdot h^T$
$\frac{\partial L}{\partial b2} = \frac{\partial L}{\partial y}$

隐藏层梯度：

$\frac{\partial L}{\partial h} = W2^T \cdot \frac{\partial L}{\partial y}$
$\frac{\partial L}{\partial z} = \frac{\partial L}{\partial h} \odot \sigma'(z)$
$\frac{\partial L}{\partial W1} = \frac{\partial L}{\partial z} \cdot x^T$
$\frac{\partial L}{\partial b1} = \frac{\partial L}{\partial z}$

4.2 手动实现反向传播

# 神经网络参数
W1 = np.random.randn(2, 3)  # 输入层到隐藏层
b1 = np.random.randn(3)
W2 = np.random.randn(3, 1)  # 隐藏层到输出层
b2 = np.random.randn(1)
learning_rate = 0.1
# 前向传播函数
def forward(x):
    z1 = np.dot(x, W1) + b1
    h = np.tanh(z1)  # 隐藏层激活
    z2 = np.dot(h, W2) + b2
    return z2, h  # 返回输出和隐藏层状态
# 反向传播函数
def backward(x, y_true, y_pred, h):
    # 计算损失梯度
    dL_dy = y_pred - y_true
    
    # 输出层梯度
    dL_dW2 = np.dot(h.T, dL_dy)
    dL_db2 = np.sum(dL_dy, axis=0)
    
    # 隐藏层梯度
    dL_dh = np.dot(dL_dy, W2.T)
    dL_dz1 = dL_dh * (1 - np.tanh(h)**2)  # tanh导数
    
    # 输入层梯度
    dL_dW1 = np.dot(x.T, dL_dz1)
    dL_db1 = np.sum(dL_dz1, axis=0)
    
    return dL_dW1, dL_db1, dL_dW2, dL_db2
# 训练数据
X = np.array([[0,0], [0,1], [1,0], [1,1]])
y = np.array([[0], [1], [1], [0]])  # XOR问题
# 训练循环
for epoch in range(10000):
    total_loss = 0
    for i in range(len(X)):
        # 前向传播
        x_in = X[i].reshape(1, -1)
        y_true = y[i].reshape(1, -1)
        
        y_pred, h = forward(x_in)
        loss = 0.5 * (y_pred - y_true)**2
        total_loss += loss.item()
        
        # 反向传播
        dW1, db1, dW2, db2 = backward(x_in, y_true, y_pred, h)
        
        # 更新参数
        W1 -= learning_rate * dW1
        b1 -= learning_rate * db1
        W2 -= learning_rate * dW2
        b2 -= learning_rate * db2
    
    if epoch % 1000 == 0:
        print(f"Epoch {epoch}, Loss: {total_loss/len(X)}")
# 测试
print("\nXOR问题测试:")
for i in range(len(X)):
    y_pred, _ = forward(X[i].reshape(1, -1))
    print(f"输入: {X[i]}, 预测: {y_pred.item():.4f}, 期望: {y[i][0]}")

4.3 反向传播可视化

graph LR
    A[输入 x] --> B[加权和 z1 = W1·x + b1]
    B --> C[激活 h = tanh z1]
    C --> D[加权和 z2 = W2·h + b2]
    D --> E[输出 y]
    E --> F[损失 L = 1/2 y-t 2]
    F -- dL/dy --> D
    D -- dL/dW2 = dL/dy·hT --> W2
    D -- dL/db2 = dL/dy --> b2
    D -- dL/dh = W2T·dL/dy --> C
    C -- dL/dz1 = dL/dh * tanh' --> B
    B -- dL/dW1 = dL/dz1·xT --> W1
    B -- dL/db1 = dL/dz1 --> b1


五、综合实例：手写数字识别

5.1 神经网络实现

import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
# 定义神经网络
class NeuralNet(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super().__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_size, output_size)
    
    def forward(self, x):
        x = x.view(x.size(0), -1)  # 展平
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)
        return x
# 加载MNIST数据集
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,), (0.3081,))
])
train_data = datasets.MNIST('./data', train=True, download=True, transform=transform)
test_data = datasets.MNIST('./data', train=False, transform=transform)
train_loader = DataLoader(train_data, batch_size=64, shuffle=True)
test_loader = DataLoader(test_data, batch_size=1000)
# 初始化模型
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = NeuralNet(28*28, 256, 10).to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
# 训练函数
def train(epoch):
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        
        # 前向传播
        output = model(data)
        loss = criterion(output, target)
        
        # 反向传播
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        if batch_idx % 100 == 0:
            print(f'Train Epoch: {epoch} [{batch_idx*len(data)}/{len(train_loader.dataset)}'
                  f' ({100.*batch_idx/len(train_loader):.0f}%)]\tLoss: {loss.item():.6f}')
# 测试函数
def test():
    model.ｅｖａｌ()
    test_loss = 0
    correct = 0
    with torch.no_grad():
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            output = model(data)
            test_loss += criterion(output, target).item()
            pred = output.argmax(dim=1, keepdim=True)
            correct += pred.eq(target.view_as(pred)).sum().item()
    
    test_loss /= len(test_loader.dataset)
    accuracy = 100. * correct / len(test_loader.dataset)
    print(f'\n测试集: 平均损失: {test_loss:.4f}, 准确率: {correct}/{len(test_loader.dataset)} ({accuracy:.2f}%)\n')
    return accuracy
# 训练循环
accuracies = []
for epoch in range(1, 11):
    train(epoch)
    acc = test()
    accuracies.append(acc)
# 可视化训练过程
plt.plot(accuracies)
plt.title('MNIST分类准确率')
plt.xlabel('Epochs')
plt.ylabel('Accuracy (%)')
plt.grid(True)
plt.show()

5.2 神经网络工作流程总结

graph TD
    A[输入数据] --> B[前向传播]
    B --> C[计算损失]
    C --> D[反向传播]
    D --> E[参数更新]
    E --> F{达到停止条件?}
    F -- 是 --> G[模型部署]
    F -- 否 --> B


关键要点总结

感知机核心公式：

输出 = f(∑(w_i * x_i) + b)

其中f为激活函数，w为权重，b为偏置

激活函数选择指南：

  • 隐藏层：优先使用ReLU及其变体（计算高效）

  • 二分类输出层：Sigmoid函数

  • 多分类输出层：Softmax函数

  • 回归输出层：线性激活（无激活函数）

损失函数选择原则：

  • 回归问题：MSE（均方误差）

  • 二分类问题：二元交叉熵

  • 多分类问题：分类交叉熵

  • 异常值处理：Huber损失

反向传播四步骤：

# 1. 前向传播计算预测值
outputs = model(inputs)
# 2. 计算损失
loss = criterion(outputs, targets)
# 3. 反向传播计算梯度
optimizer.zero_grad()  # 清空历史梯度
loss.backward()        # 自动计算梯度
# 4. 更新参数
optimizer.step()       # 根据梯度更新权重

神经网络设计原则：

  • 输入层节点数 = 特征维度

  • 输出层节点数 = 类别数（分类）或1（回归）

  • 隐藏层节点数：64-1024（根据问题复杂度调整）

  • 隐藏层数量：1-3层（简单问题），>10层（深度学习）


通过掌握这些神经网络基础，你已经为学习卷积神经网络、循环神经网络等高级模型奠定了坚实基础！更多AI大模型应用开发学习视频内容和资料，尽在聚客AI学院。


版权声明：倡导尊重与保护知识产权。未经许可，任何人不得复制、转载、或以其他方式使用本站《原创》内容，违者将追究其法律责任。本站文章内容，部分图片来源于网络，如有侵权，请联系我们修改或者删除处理。

相关阅读：

神经网络基础深度解析：从感知机到反向传播

PyTorch深度学习入门实战指南：从张量到神经网络

机器学习基础概念深度解析：从理论到实战

企业级知识库问答系统实战：从架构到部署的完整指南

大模型微调与部署终极指南：从LoRA到GGUF的工业级实践

Transformer架构完全拆解：从数学公式到工业级代码的终极实践手册

编辑推荐

热门文章

大厂标准培训
海量精品课程
汇聚优秀团队
打造完善体系
Copyright © 2023-2025 聚客AI 版权所有
网站备案号：湘ICP备2024094305号-1